Precise Qualifier in GLSL and NVIDIA GeForce Cards (***Updated***)

---

Note: I wrote the original article in french some months ago. I didn’t tested with recent drivers but I think the content of the article is still valid. Hope that helps!

---

The keyword (or qualifier) precise in GLSL (introduced with the GL_ARB_gpu_shader5 extension) allows to specify to the GLSL compiler to not apply optimizations on the computations of a variable. Especially, some situations require that floating-point computations have to be executed in the exact order specified by the developer in the GLSL source code. With floating point computations, a*b*c may be different from a*c*b due to rounding errors.

Section 4.Q, The Precise Qualifier

Some algorithms may require that floating-point computations be carried
out in exactly the manner specified in the source code, even if the
implementation supports optimizations that could produce nearly equivalent
results with higher performance. For example, many GL implementations
support a “multiply-add” that can compute values such as

float result = (float(a) * float(b)) + float(c);

in a single operation. The result of a floating-point multiply-add may
not always be identical to first doing a multiply yielding a
floating-point result, and then doing a floating-point add. By default,
implementations are permitted to perform optimizations that effectively
modify the order of the operations used to evaluate an expression, even if
those optimizations may produce slightly different results relative to
unoptimized code.

The qualifier “precise” will ensure that operations contributing to a
variable’s value are performed in the order and with the precision
specified in the source code. Order of evaluation is determined by
operator precedence and parentheses, as described in Section 5.
Expressions must be evaluated with a precision consistent with the
operation; for example, multiplying two “float” values must produce a
single value with “float” precision. This effectively prohibits the
arbitrary use of fused multiply-add operations if the intermediate
multiply result is kept at a higher precision. For example:

precise out vec4 position;

declares that computations used to produce the value of “position” must be
performed precisely using the order and precision specified.

I tested the precise keyword in some GLSL shaders when I was looking for the solution of a tessellation bug in MSI Kombustor 2.2.0. But actually, the bug wasn’t related to rounding errors or other optimizations made by the compiler. I fixed the bug later but it’s not the topic here. The problem is that I forgot a precise keyword in one of the tessellation shaders when I was cleaning my GLSL code. And at this moment of development, I had a Radeon HD 6870 in my PC… No no no, the Radeon was not the problem, actually it was rather cool to code with it, and there was no problem with this precise leftover. So what was the problem?

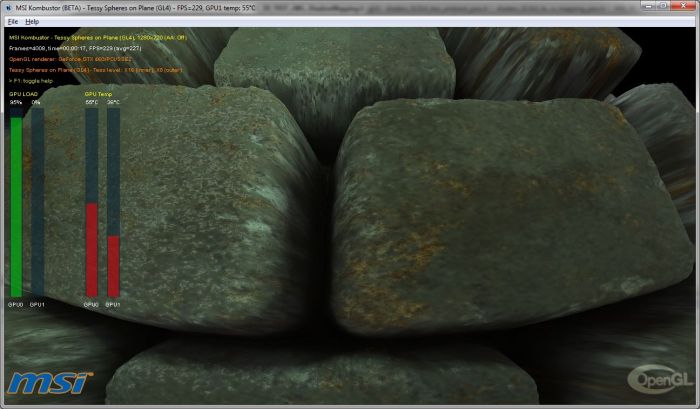
Several days after, I replaced the HD 6870 by a GeForce GTX 460 and I got this nice leopard-skin like rendering:

The black spots come from the precise keyword I forgot in a shader…

In Kombustor, there are several 3D tests that feature tessellation + soft shadows. Quickly said, the soft shadow algorithm uses two passes: a first pass to initialize the z-buffer and draw the scene with ambient light only, and a second pass (called illumination pass) to shade the pixels according to the shadow map. This second pass is rendered using glDepthFunc(GL_EQUAL) (as well as some additive blending) to color the necessary pixels only.

The rendering with GL_EQUAL works fine if the vertices computed in the second pass have exactly the same position than those computed in the first pass. But in Kombustor, I forgot a the precise qualifier in one of the illumination pass shaders (in the TES, Tessellation Evaluation Shader). What does it mean? Simply that no optimization is applied on the variable with precise while in the corresponding TES shader in the ambient pass, the GLSL compiler has applied some optimizations on the same variable. On Radeon cards (HD 6800 and HD 6900), there was absolutly no problem but that was fatal on GeForce cards.

The vertices positions computed in the second pass were slightly different (from the first pass) because of the precise qualifier. Some pixels of the second pass ended up with a Z coordinate that was different from the one computed in the first pass. And the GL_EQUAL depth test has filtered those pixels with bad Z coordinate, resulting in dark spots at the places where pixels have incorrect Z.

I wasted some hours on this nasty bug and once I realized that precise was the source of all my worries, I was happy to say hello to the correct rendering:

The précise keyword has much more influence on the optimizations done by NVIDIA’s GLSL compiler than by AMD one. Why such a difference with Radeon boards? Is there a bug somewhere?

---

Update: Graham Sellers, the OpenGL guy at AMD, sent me this reply:

“The précise keyword has much more influence on the optimizations done by NVIDIA’s GLSL compiler than by AMD one. Why such a difference with Radeon boards? Is there a bug somewhere?”

Nope, I think you just got lucky. We do honor the precise keyword. However, it just tells us to not optimize the expression. It’s possible that we missed a potential optimization that the NVIDIA compiler was able to do, or that we optimized in a way that didn’t affect the result. However, it’s totally possible that this could have affected our compiler, or that we would implement more aggressive optimization in the future and that it would have broken your application.