Rendu de l’Attracteur de Lorenz (et Effet Papillon)

Comme l’éponge de Menger ou la fractale de Mandelbrot, la représentation graphique de l’attracteur de Lorenz est relativement populaire.

Les équations de l’attracteur (dites équations de Lorenz) ont été mises au point par Edward Norton Lorenz, alors météorologue au MIT lorsqu’il travailla sur des problèmes complexes de mouvement d’air dans l’atmosphère.

Tous ces détails chaotiques me dépassant un peu, je n’irai pas plus loin dans la théorie (pour ça allez embêter le Dr Goulu de ma part). Ce qui m’intéresse ici ce sont les équations simplifiées de Lorenz qui permettent de faire un rendu graphique de l’attracteur. Ce système de trois équations décrit une trajectoire dans l’espace 3D. Ces équations sont les suivantes:

dx/dt = S(y - x)
dy/dt = x(R - z) - y
dz/dt = xy - Bz

En gros, ces équations décrivent quelle est la valeur de la variation de position (dx, dy et dz) dans l’espace 3D pour une petite variation de temps (dt). Au niveau programmation 3D, cette petite variation de temps est le time_step d’une frame par example. Il suffit d’avoir une position initiale différente de (0;0;0) sinon il ne se passe rien, d’injecter x, y, et z dans ces équations et d’ajouter dx, dy et dz à la valeur de la position. On recommence avec la position nouvellement obtenue en entrée des équations et ainsi de suite.

S, R et B sont les paramètres de ce système d’équations et l’on obtient la fameuse trajectoire de l’attracteur de Lorenz pour:
– S = 10
– R = 28
– B = 8/3

Voici un pseudo algo (en pseudo Lua) pour tracer la trajectoire. Soit dt la durée d’une frame et P la position 3D:

function InitPosition()
  P.x = random()
  P.y = random()
  P.z = random()
end

function UpdatePosition(dt)
  dx = 10 * (P.y - P.x) * dt
  dy = (P.x * (28 - P.z) - P.y) * dt
  dz = (P.x * P.y - 8/3 * P.z) * dt

  P.x = P.x + dx
  P.y = P.y + dy
  P.z = P.z + dz
end


InitPosition()
while(true)
  UpdatePosition(dt)
  DrawPoint(P)
end

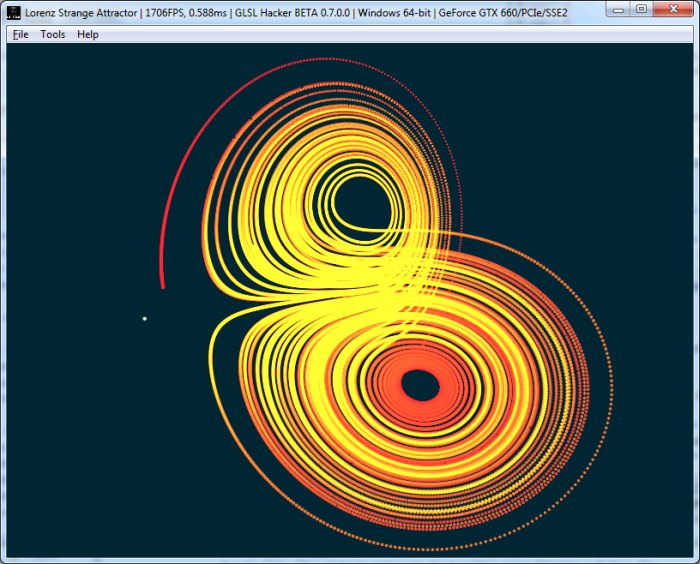
L’Effet Papillon (butterfly effect): un battement d’aile de papillon dans un coin du monde peut provoquer un ouragan dans un autre coin du monde. Plus simplement, une petite variation de la position initiale (par exemple de 0.01) conduira à deux trajectoires différentes et imprévisibles. Les deux figures suivantes montrent cette différence (où la différence entre les deux positions est justement de 0.01 au niveau de chaque coordonnée):

Effet Papillon – P0={x=2.0; y=2.02; z=2.0} – S=10, R=28 and B=8/3:

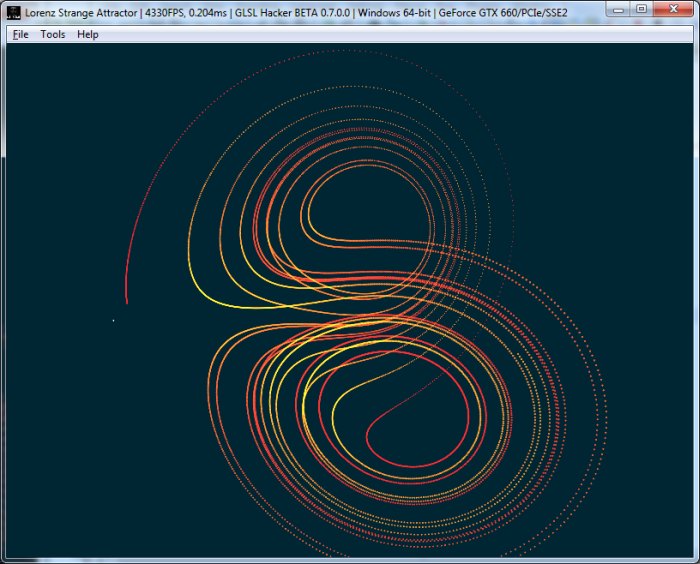
Effet Papillon – P0={x=2.01; y=2.03; z=2.01} – S=10, R=28 and B=8/3:

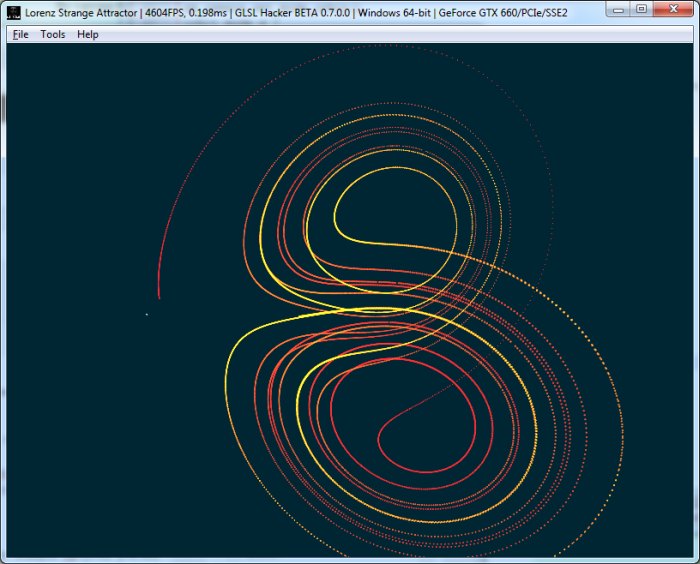
La forme de la trajectoire ressemblant aux ailes d’un papillon, le nom d’effet papillon a été donné à cet effet d’amplication.

Les ailes d’un papillon

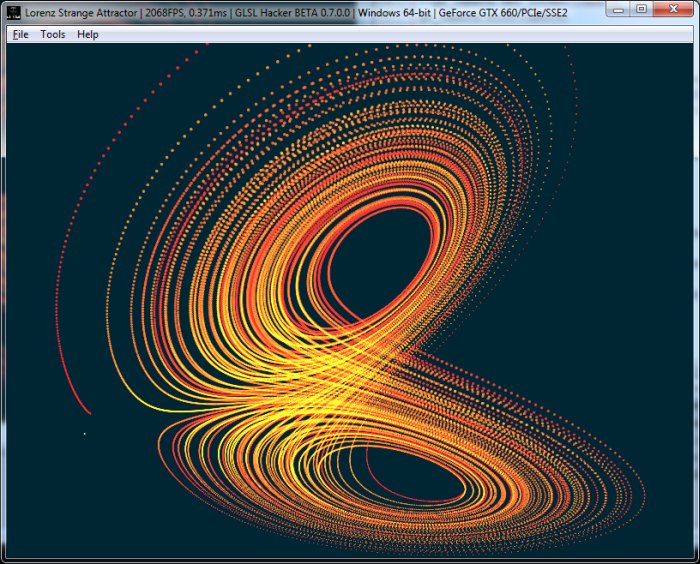
J’ai préparé une petite demo avec GLSL Hacker qui permet de visualiser la trajectoire d’un point qui évolue selon les équations de Lorenz. Et pour rendre la demo plus intéressante du point de vue visuel, chaque position est affichée ce qui permet de voir la trajectoire complete et non juste le mouvement d’un point:

La démo est disponible dans le répertoire host_api/Particle_Lorenz_Attractor/ du pack de démos. Pour exécuter la demo, il suffit de lance GLSL Hacker et de glisser la demo XML dans la fenêtre de GLSL Hacker (le drag-n-drop est disponible pour les versions Windows et Mac OS X de GLSL Hacker. Pour Linux, il faut éditer un petit fichier en spécifiant le chemin d’accès au fichier de demo).

La demo est codée en Lua et utilise un vertex pool (en gros un big tableau de particules) associé à un petit programme GLSL de rendu de particules.

Pour changer la valeur de la position initiale, aller voir autour de la ligne 80 du code source de la demo. Pour changer les paramètres S, R et B des équations de Lorenz, faites un saut à la ligne 180.

Attracteur de Lorenz pour S=12, R=30 and B=2:

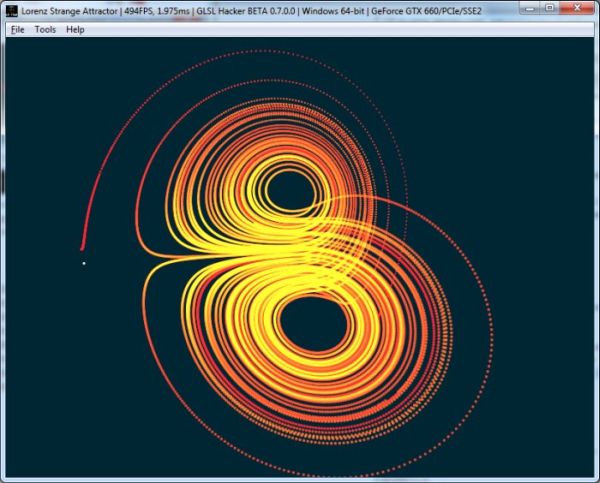
Attracteur de Lorenz pour S=45, R=45 and B=8/3:

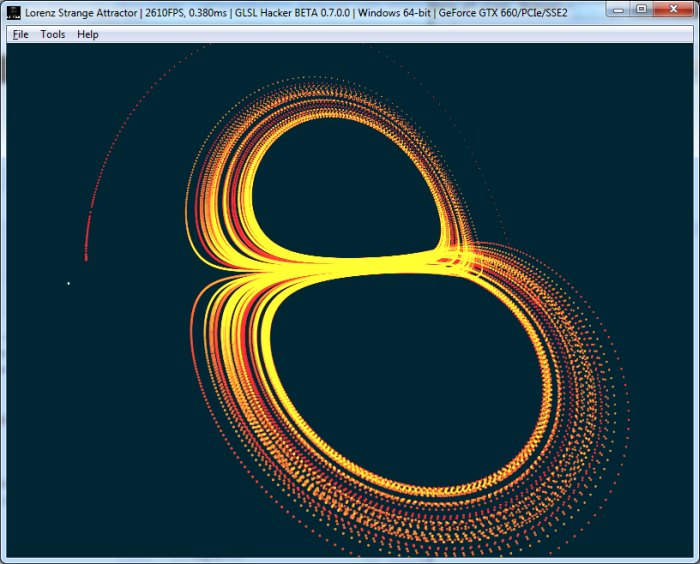
Attracteur de Lorenz pour S=10, R=30 and B=4.5:

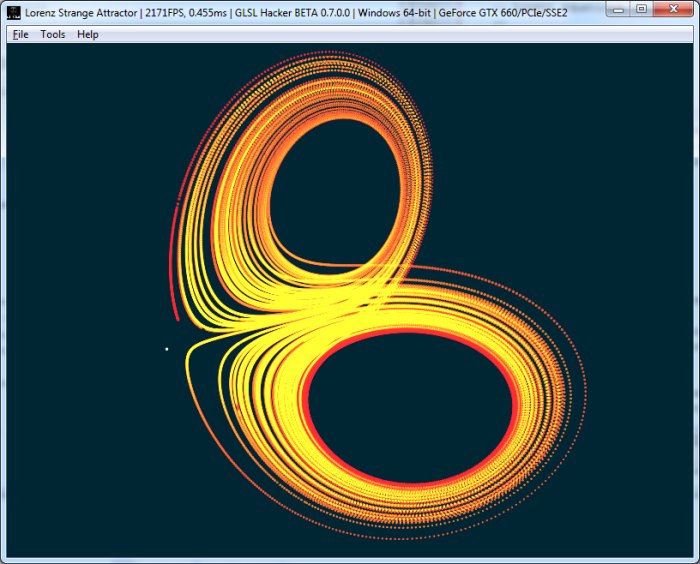
Quelques réferences:
– Butterfly effect
– The Lorenz Attractor in 3D
– The Lorenz attractor (AKA the Lorenz butterfly)